Определение. Производной функции 
в точке 
называется предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю.
Обозначают 
Правила вычисления производных
1. 
, 2. 
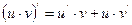, 3.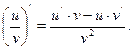 
Таблица производных
1. 
2. 
3. 
4. 
5. 
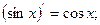
6. 
7. 
8. 
9. 
10. 
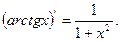
Пример 1. Используя правила и формулы дифференцирования найти производные функций: 1)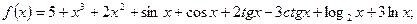 
2) 
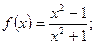3) 
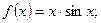4) 
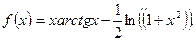
Решение.
1) 
2) 
3) 
4) 
Пример 2. Определить глобальные экстремумы 
Решение.
Ответ: 
Пример 3. Исследовать на монотонность, найти локальные экстремумы и построить эскиз графика функции 
Решение.
точки экстремума,
-экстремумы функции,
- промежутки возрастания,
- промежутки убывания.
Пример 4. Найти промежутки выпуклости и точки перегиба функции
Решение.
- точка перегиба.
- выпуклость направленная вверх.
- выпуклость направленная вниз.
Пример 5. Провести полное исследование свойств и построить эскиз графика функции
Решение.
- вертикальная асимптота.
- горизонтальная асимптота
- функция нечетная
Точки пересечения с осями:
с ох, у=0 – нет точек, с оу, х=0 – нет точек.
Точки экстремума:
- точки экстремума,
-экстремумы функции.
Точки перегиба:
- точка перегиба.
