|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Фрейм мерседес-бенц в в-мерном пространствеДата добавления: 2015-09-15; просмотров: 1288; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

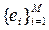 в
в 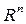 называется жёстким фреймом в
называется жёстким фреймом в 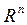 если существует число А > 0 такое, что для любого вектора
если существует число А > 0 такое, что для любого вектора 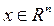 выполнено равенство
выполнено равенство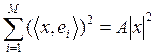 (3)
(3)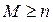 . Каждый вектор
. Каждый вектор 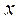 можно разложить по фрейму. Действительно, в силу (3) справедливо тождество
можно разложить по фрейму. Действительно, в силу (3) справедливо тождество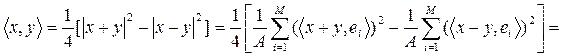
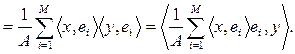
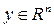 , то
, то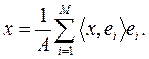 (4)
(4)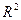 , состоящий из трёх векторов единичной длины, расположенных под углом 120°.
, состоящий из трёх векторов единичной длины, расположенных под углом 120°.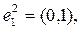
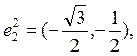
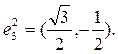 (5)
(5)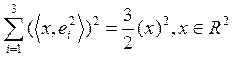
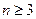 можно построить аналогичную конструкцию в
можно построить аналогичную конструкцию в 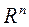 , которая называется каноническим фреймом Мерседес-Бенц.
, которая называется каноническим фреймом Мерседес-Бенц.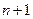 векторов
векторов 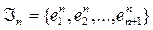 со свойствами:
со свойствами: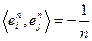 ,
, 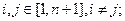
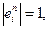
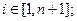
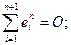
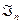 является жёстким фреймом с константой
является жёстким фреймом с константой 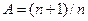 .
.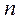 . При
. При 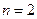 фрейм (5) удовлетворяет всем утверждениям теоремы.
фрейм (5) удовлетворяет всем утверждениям теоремы.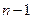 все утверждения выполнены. Система
все утверждения выполнены. Система 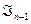 с помощью процедуры добавления.
с помощью процедуры добавления.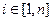 вектор
вектор 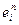 строится из
строится из 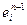 добавлением
добавлением 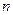 -й компоненты-
-й компоненты- 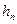 и нормированием получившегося вектора:
и нормированием получившегося вектора: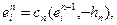 где
где 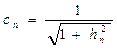
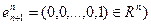 . По индуктивному предположению.
. По индуктивному предположению.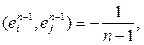
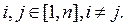
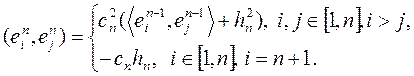
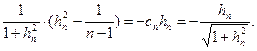
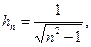
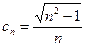 .
.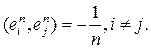 Имеем
Имеем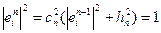 ,
, 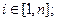
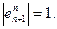
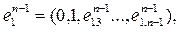
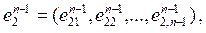 ….
…. 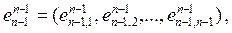
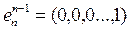 .
.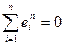 .
.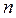 следующим образом:
следующим образом: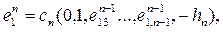
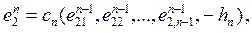 ….
…. 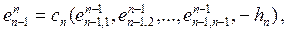
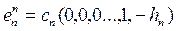 ,
,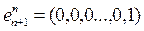 .
.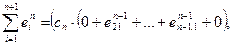
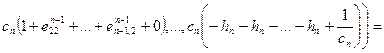
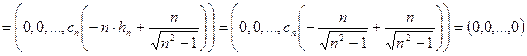 .
.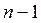 система векторов
система векторов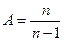 . Тогда для вектора
. Тогда для вектора 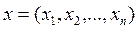 имеет место
имеет место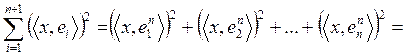
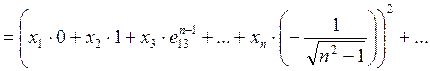
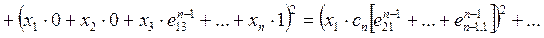
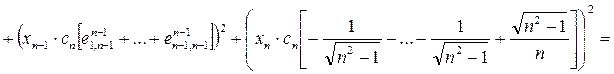
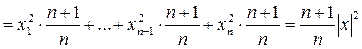
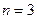 применяя имеющийся фрейм при
применяя имеющийся фрейм при 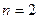 .
.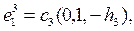
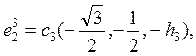
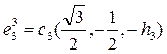 ,
, 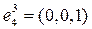 .
.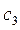 и
и 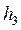 .
.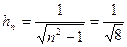 ,
, 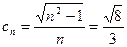 .
.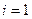 . Тогда для
. Тогда для 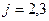 имеем
имеем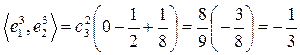 ,
, 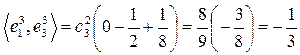 .
.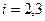 аналогично.
аналогично.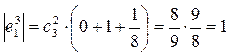 ,
, 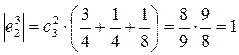 ,
,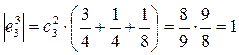 ,
, 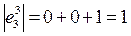 .
.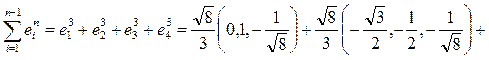
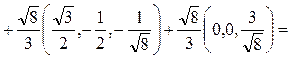
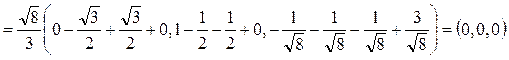 .
.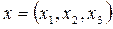 . Тогда
. Тогда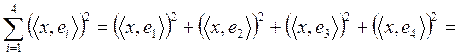
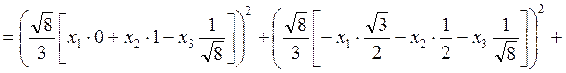
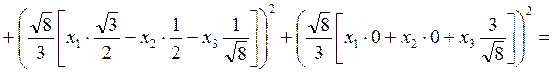
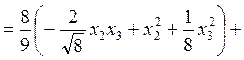
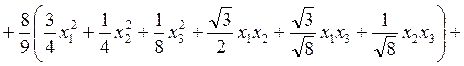
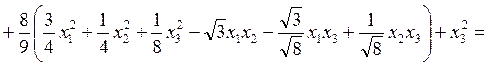
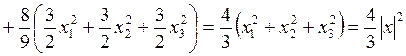 .
.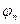 между двумя различными векторами
между двумя различными векторами 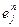 находится из условия
находится из условия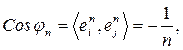
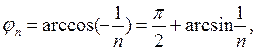
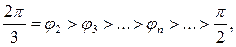
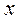 по коэффициентам
по коэффициентам 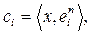
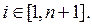 Если любой из коэффициентов
Если любой из коэффициентов 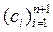 будет утрачен, то по оставшимся вектор
будет утрачен, то по оставшимся вектор 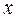 восстановить можно.
восстановить можно.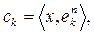 с некоторым номером
с некоторым номером 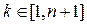 . Рассмотрим систему
. Рассмотрим систему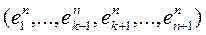 (6)
(6)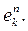 В системе (6) скалярное произведение двух различных векторов равно
В системе (6) скалярное произведение двух различных векторов равно 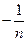 , а норма каждого вектора равна 1. Поэтому матрица Грамма системы (6) имеет вид
, а норма каждого вектора равна 1. Поэтому матрица Грамма системы (6) имеет вид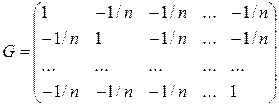
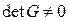 и, значит, система (6) линейно независима. Поэтому существует единственная система
и, значит, система (6) линейно независима. Поэтому существует единственная система 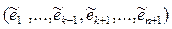 , биортогональная к (6), и вектор
, биортогональная к (6), и вектор 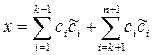 .
.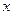 в случае, когда часть фреймовых коэффициентов утрачена, рассматривался во многих работах (см., например, [3]). Там же использовалось название «Mercedes-Benz frame».
в случае, когда часть фреймовых коэффициентов утрачена, рассматривался во многих работах (см., например, [3]). Там же использовалось название «Mercedes-Benz frame».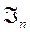 можно получить другие жесткие фреймы. Умножим все векторы фрейма на произвольную ортогональную матрицу Q и перед получившимися векторами в произвольном порядке расставим знаки + и —:
можно получить другие жесткие фреймы. Умножим все векторы фрейма на произвольную ортогональную матрицу Q и перед получившимися векторами в произвольном порядке расставим знаки + и —: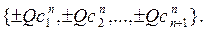 (7)
(7)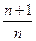 состоящий из
состоящий из