1. Математическое ожидание постоянной равно самой этой постоянной: 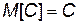 .
.
В самом деле, закон распределения постоянной СВ имеет вид
поэтому, по определению математического ожидания 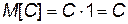 .
.
2. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых 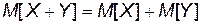
3. Постоянный множитель можно выносить за знак математического ожидания: 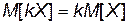 .
.
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: 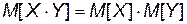 .
.
5. Математическое ожидание неотрицательной СВ неотрицательно и равно нулю тогда и только тогда, когда СВ равна нулю.
Замечание. Математическое ожидание СВ есть некоторое среднее, вокруг которого группируются значения, принимаемые СВ. Однако, легко указать такие случайные, которые имеют одинаковые математические ожидания, но различные принимаемые значения. Более того, эти значения могут совершенно по-разному группироваться вокруг математического ожидания. Например: математические ожидания СВ
очевидно, равны нулю, однако значения СВ Хгораздо менее удалены от математического ожидания, чем значения СВ У. Для описания величины разброса значений СВ применяют числовую характеристику, называемую дисперсией.