С понятием полноты тесно связано понятие замыкания. Пусть MÍ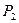 
. Замыканием [M] множества M называется множество всех булевых функций, представимых формулами над M. Теперь определение полноты можно переформулировать следующим образом. Система функций MÍ 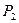полна в 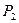, если [M]= .
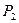Множество M называется замкнутым классом, если [M]=M.
Пример 9.
– [ ]= ;
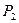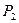– [{Ø,&,Ú}]= ;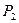
– [{0,1}]=[{0,1}].
Свойства замыкания:
1. MÍ[M].
2. [M]=[[M]].
3. Если M1ÍM2, то [M1]Í[M2].
4. [M1]È[M2]Í [M1ÈM2].
Задачи
22.Сведением к заведомо полным системам показать, что множество A является полным в P2:
22.1.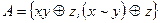 
;
22.2.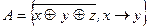 
;
22.3.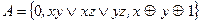 
;
22.4.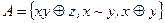 
;
22.5.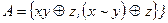 
;
22.6.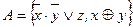 
;
22.7.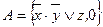 
;
22.8.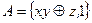 
;
22.9.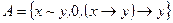 
;
22.10.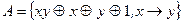 
.
