Система функций {f1,f2,…,fi,…} из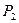 
называется полной в 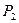, если любая булева функция может быть представлена в виде суперпозиции функций данной системы.
Теорема 4.Пусть {f1,f2,…,fi,…} – полная в 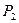система, а {g1,g2,…,gK,…} – такая система функций, что для любого i fi=Si[g1,g2,…,gK,…]. Тогда система {g1,g2,…,gK,…} – полна.
Пример 8. Полными в 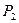являются системы:
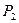– (т.к. каждую функцию можно считать формулой над );
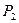– {Ø,&,Ú} (в силу теоремы 2);
– {0,1,&,Å} (т.к. система {Ø,&,Ú} полна и xÚy=x&yÅxÅy).
– {Ø,&} (т.к. система {Ø,&,Ú} полна и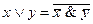 
);
– {Ø,Ú} (т.к. система {Ø,&,Ú} полна и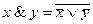 
);
– {|} (т.к. система {Ø,&} полна и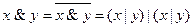 
, 
).
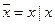