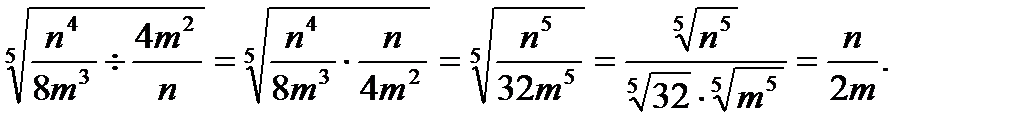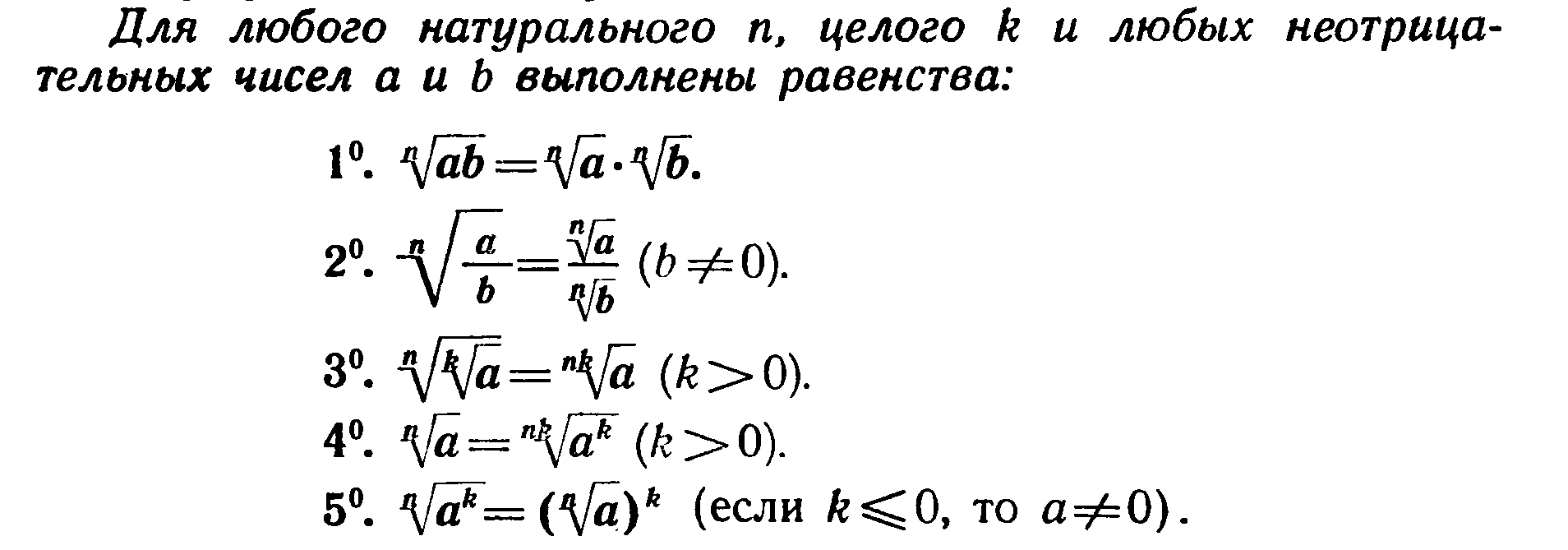
Для арифметического корня n-й степени, как и для квадратного корня, существуют операции внесения множителя под знак корня и вынесение множителя из-под знака корня.
Например :
2 
.
Из примера видно, что для внесения множителя под знак корня n-й степени его нужно
возвести в n-ю степень. Нужно помнить, что под знак с четным показателем мы имеем право внести только положительный множитель, например:
Аналогично производится вынесение множителя из-под знака корня , например:
а)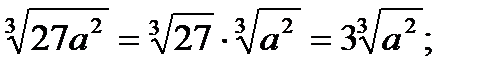 
б)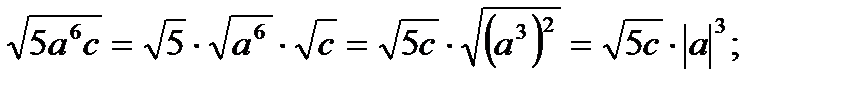 
в)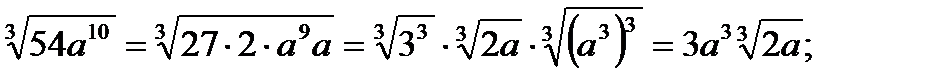 
Примеры решения упражнений:
№1
Вычислить:
а) 
; б) 
; в) 
г)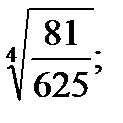 
Решение:
а) =- 
; б) =2;
в) 
= 
; г)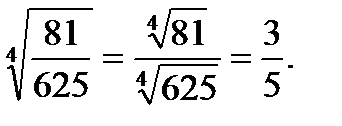 
№2
Решить уравнение:
а)х6=5; б) х3=5; в) 0,01х3+10=0.
Решение:
а) х6=5;
так как 6- четное число, то уравнение имеет два корня
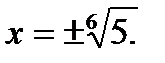
Ответ: 
.
б) х3=5;
так как 3-нечетное число, то уравнение имеет один корень.
.
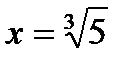Ответ: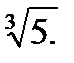 
в) 0,01х3+10=0;
0,01х3=-10;
х3= 
;
х3= 
;
х3=-10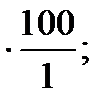 
х3=-1000;
х=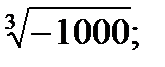 
х=-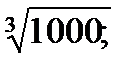 
х= -10.
Ответ :-10.
№3
Вычислить:
а) 
; б) 
; в) 
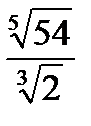; в) 
.
Решение:
а) = 
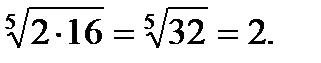
б)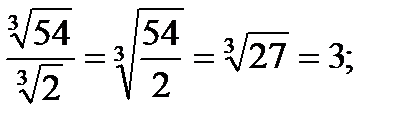 
в)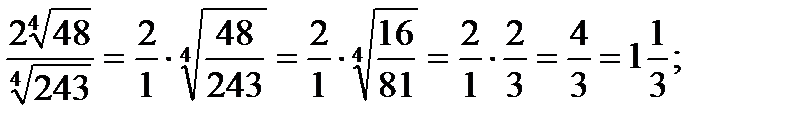 
г)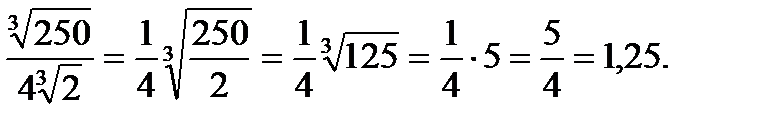 
№4
Упростите выражение:
а) 
; б) 
если х>0;
в) 
если к>0 ; г)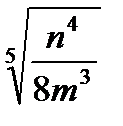 
: 
.
Решение:
а) = 
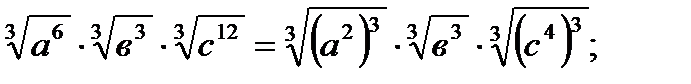
так как 3- нечетное число, получим
а2вс4.
Ответ: а2вс4.
б) = 
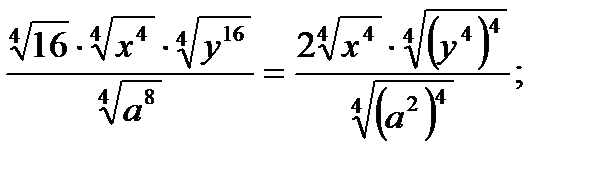
Так как 4-нечетное число, то получим
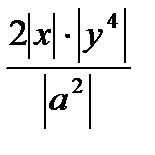
Так как х>0 по условию, то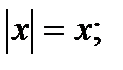 
у4≥0 (так как 4-четное число), следовательно 
,
аналогично рассуждая, получим 
.
Итого получим:
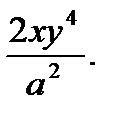
Ответ: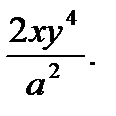 
в) = 
= 
;
так как к>0, то к6>0, следовательно 
.
Итого получим:
.
Ответ: 
.
г) : =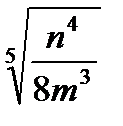 
