Если функция у аргумента х задана параметрическими уравнениями
то 
.
Формула Тейлора (к заданию №4)
Если функция y=f(x) имеет производные до (n+1)-го порядка включительно в некоторой δ-окрестности точки а (δ(а)), то для всякого х 
δ(а) справедлива формула
,
,
где ξ=a+θ(x-a), причем 0<θ<1,
при а=0 получается формула Маклорена
,
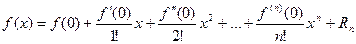, 0<θ<1.
Разложение некоторых функций по формуле Маклорена:
Неопределенный интеграл (к заданию №5)
Функция F(x) называется первообразной от функции f(x)на [a, b],если 
выполняется равенство F'(x)=f(x).
Теорема. Если F1(x) и F2(x) – две первообразные от функции f(x) на [a, b], то разность между ними равна постоянному числу.
Если F(x)является первообразной для f(x),то выражение F(x)+С называется неопределенным интегралом от f(x)и обозначается символом ∫f(x)dx, то есть ∫f(x)dx=F(x)+C.
При этом функцию f(x) называют подынтегральной, f(x)dx – подынтегральным выражением, знак ∫ - знаком интеграла.
Некоторые свойства неопределенного интеграла
1. 
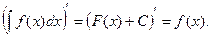
2. 
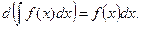
3. 
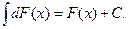
4. 
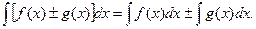
5. 
где a=const.
6. 
где a, b – const.
,
.
,
.
,
.
,
.