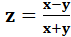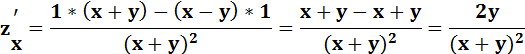Пусть задана функция z = f(х, у). Так как х и у – независимые переменные, то одна из них может изменяться, а другая сохранять постоянное значение. Дадим переменной хприращение ∆х, сохраняя значение переменной у неизменным. Тогда функция zполучит приращение, которое назовем частным приращением z по х и обозначим
∆х z: ∆х z = f(x + ∆x, y) – f(х, у).
Аналогично получаем частное приращение z по у:
∆у z = f(x, у + ∆ y) – f(х, у).
Наконец, если аргументу х дать приращение ∆х, а аргументу у – приращение ∆у, то получим полное приращение функции z:
∆ z=f(x+∆x, y+∆у)–f(х, у).
Надо заметить, что полное приращение функции, вообще говоря, не равно сумме частных её приращений, т.е. ∆z ≠ ∆х z + ∆у z.
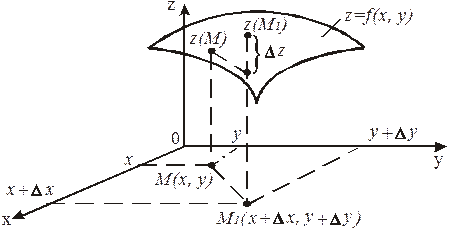
Геометрически полное приращение функции ∆z равно приращению аппликаты графика функции z = f(х, у) при переходе от точки М(х, у) к точке М1 (х + ∆х, у + ∆у) (рис. 5).
Определение. Полным дифференциалом функции многих переменных называется главная линейная относительно приращений аргументов часть малого полного приращения функции.
Рассмотрим функцию двух переменных n=2; z=f(x,y). Если приращение функции  можно представить в виде
можно представить в виде 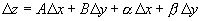
где  - бесконечно малые функции при
- бесконечно малые функции при  , соответственно, то выражение
, соответственно, то выражение  называется полным дифференциалом функции двух переменных.
называется полным дифференциалом функции двух переменных.
Теорема. Полный дифференциал равен сумме попарных произведений частных производных на дифференциалы соответствующих переменных.
 .
.
Пример.  .
.
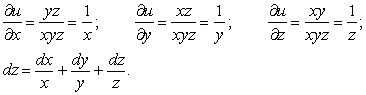
3.

4.