Допустим что функции sinx и cosx входят в тригонометрическое уравнение только рационально. Такие тригонометрические уравнения назовем рациональными тригонометрическими уравнениями . Если все члены такого уравнения перенесены в его левую часть, то в общем виде его можно записать так: 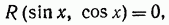
где R - символ совокупности рациональных операций, которые нужно произвести над sinx и cosx.
Приведем примеры рациональных тригонометрических уравнений, а также тригонометрических уравнений, которые таковыми не являются.
1) Уравнение  , является рациональным тригонометрическим уравнением, так как
, является рациональным тригонометрическим уравнением, так как 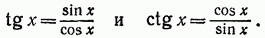
2) Уравнение  , не является рациональным тригонометрическим уравнением, ибо в число операций, которые производятся над тригонометрическими функциями, содержащими аргумент x входит не рациональная операция — извлечение кубического корня.
, не является рациональным тригонометрическим уравнением, ибо в число операций, которые производятся над тригонометрическими функциями, содержащими аргумент x входит не рациональная операция — извлечение кубического корня.
3) Уравнение  , является рациональным тригонометрическим уравнением.
, является рациональным тригонометрическим уравнением.
4) Уравнение  , не является рациональным тригонометрическим уравнением, ибо в число операций, которые производятся над тригонометрическими функциями, содержащими аргумент х, входят не рациональные операции — операция взятия синуса от
, не является рациональным тригонометрическим уравнением, ибо в число операций, которые производятся над тригонометрическими функциями, содержащими аргумент х, входят не рациональные операции — операция взятия синуса от  и операция взятия косинуса от
и операция взятия косинуса от  .
.
Теорема. Рациональное уравнение 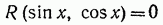 , с помощью тригонометрической подстановки
, с помощью тригонометрической подстановки  , приводится к рациональному уравнению
, приводится к рациональному уравнению  относительно новой неизвестной t.
относительно новой неизвестной t.