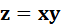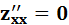Если каждой точке M(x1, x2,…, xn) множества G точек n-мерного евклидова пространства
En по некоторому закону поставлено в соответствие определенное действительное число
u, то говорят, что на множестве G определена функция точки М или функция n
переменных x1, x2,…, xn, и пишут u=f(M), или u=f(x1, x2,…, xn), М∈G.
Множество G называется областью определения функции f.
Если функция задана одним аналитическим выражением, причем область определения
функции заранее не указана, то в качестве области определения принимают совокупность
всех тех точек M(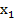 
, 
,…, 
), для которых данное аналитическое выражение имеет
конечное действительное значение (естественная область определения). Так, для функции
z=x+y область определения – вся плоскость xOy, для функции z= 
область определения – замкнутый круг 
≤1.
Определение. Число А называется пределом функции f(M) в точке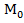 
( 
, 
), если для
любого числа ε>0 существует число δ>0 такое, что для всех точек M(x, y)∈Ω, отличных от
точки 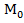( , ) и удовлетворяющих условию 0<ρ(M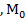 
)<δ, верно неравенство
|f(M)-A|<ε (1) (определение по Коши).
Определение. Функция f(M) называется непрерывной в точке 
( , ), если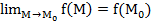 
или, что то же,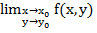 
или функция f(M) непрерывна в
точке , если для всякого ε>0 существует δ>0 такое, что для всех точек M∈Ω, таких, что
ρ(M,)<δ , выполняется неравенство |f(M)-f 
, |<ε.
3. 
4. 
