Частные производные функции нескольких переменных являются функциями тех же переменных. Эти функции, в свою очередь, могут иметь частные производные, которые мы будем называть вторыми частными производными (или частными производными второго порядка) исходной функции. Так, например, функция -1- двух переменных имеет четыре частных производных второго порядка, которые определяются и обозначаются следующим образом:  .
.
Функция -2- трех переменных имеет девять частных производных второго порядка:
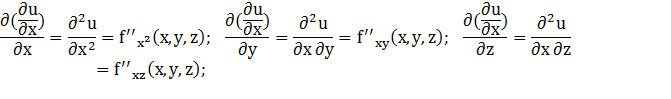
Аналогично определяются и обозначаются частные производные третьего и более высокого порядка функции нескольких переменных: частной производной -3- порядка функции нескольких переменных называется частная производная первого порядка от частной производной -4- порядка той же функции.
Например, частная производная третьего порядка функции -5- есть частная производная первого порядка по у от частной производной второго порядка -6-.
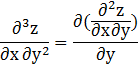
Частная производная второго или более высокого порядка, взятая по нескольким различным переменным, называется смешанной частной производной.
Например, частные производные
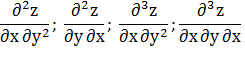
являются смешанными частными производными функции двух переменных .
3. 
4.  ;
; 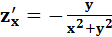 ;
;  ;
;



