Примеры интегрирования рациональных функций.
Рассмотрим интеграл вида 
, где 
— рациональная функция. Всякое рациональное выражение 
можно представить в виде 
, где 
и 
— многочлены. Если эта дробь неправильная, т. е. если степень числителя больше или равна степени знаменателя, то ее можно представить в виде суммы многочлена (целая часть) и правильной дроби. Поэтому достаточно рассмотреть интегрирование правильных дробей.
Покажем, что интегрирование таких дробей сводится к интегрированию простейших дробей, т. е. выражений вида:
1) 
где A,B,a,p,q — действительные числа, а квадратный трехчлен 
не имеет действительных корней. Выражения вида 1) и 2) называют дробями 1-го рода, а выражения вида 3) и 4) — дробями 2-го рода.
Интегралы от дробей 1-го рода вычисляются непосредственно
1) 
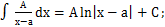
2) 
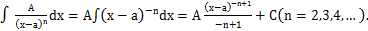
Рассмотрим вычисление интегралов от дробей 2-го рода: 3)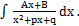 
Сначала заметим, что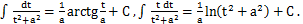 
Чтобы свести вычисление интеграла 3) к этим двум интегралам, преобразуем квадратный трехчлен , выделив из него полный квадрат: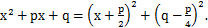 
Так как по предположению этот трехчлен не имеет действительных корней, то 
и мы можем положить 
. Подстановка 
преобразует интеграл 3) к линейной комбинации указанных двух интегралов: )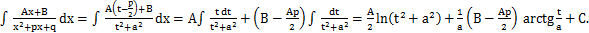 
В окончательном ответе нужно лишь заменить t на 
, а a на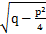 
. Так как 
, то
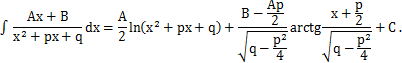
Рассмотрим случай 4) 
.
Как и в предыдущем случае, положим 
. Получим: 
.
Первое слагаемое вычисляется так: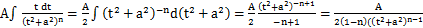 
Второй же интеграл вычисляется с помощью рекуррентной формулы.
