Если функция 
и ее частные производные 
и 
определены и непрерывны в некоторой в некоторой окрестности точки
и при этом 
, а 
, то уравнение 
определяет в некоторой окрестности точки единственную неявную функцию 
, непрерывную и дифференцируемую в некотором интервале, содержащем точку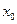 
, причем 
.
Пусть левая часть уравнения удовлетворяет указанным в теореме условиям. Тогда это уравнение определяет неявную функцию , для которой в окрестности точки имеет место тождество 
относительно 
.
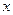Так как производная функции, тождественно равной нулю, также равна нулю, то полная производная 
, откуда 
По этой формуле находится производная неявной функции.
Пример.
Найти производную неявной функции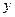 
, заданной уравнением: 1) 
.
Введем обозначение = 
Тогда 
Следовательно, 
.
2) 
.
,
Следовательно,
.
Производная по направлению
