= 
.
Рассмотрим теперь функцию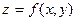 
при условии, что 
.
Тогда 
.
Пример.Найти 
, где 
, 
, 
.
Предположим теперь, что 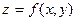, причем 
, тогда из формулы ( 5 ) получим: 
аналогично,
. ( 6 )
Пример.Найти 
и 
, где 
.
= 
, 
= 
, 
, 
, 
, 
.
= 
, 
.
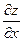Инвариантность формы полного дифференциала
Как известно, для дифференциала функции одной переменной 
имеет место инвариантность его формы. Это значит, что выражение для дифференциала 
остается верным независимо от того, является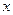 
независимой переменной или функцией некоторой переменной: 
.
Для функции нескольких переменных справедливо аналогичное утверждение.
Для доказательства ограничимся функцией двух переменных .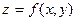
Как известно, полный дифференциал имеет следующий вид:
.
Покажем, что эта форма дифференциала сохраняется, когда 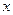и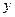 
становятся функциями новых переменных: 
Тогда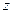 
является сложной функцией 
. Дифференциал этой сложной функции выражается формулой 
.
Но по формулам ( 6 ) 
.
Следовательно,
= . Так как 
, а 
.
Что и требовалось доказать.
