Пусть дана функция 
, причем 
Будем предполагать, что функции 
имеют производные в точке 
, функция в соответствующей точке 
дифференцируема.
Пусть независимая переменная получает приращение 
; тогда переменные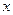 
и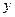 
получат соответствующие приращения 
и 
, а функция 
приращение 
.
Тогда 
. ( 3 )
Разделим обе части равенства (3) на и переходя к пределу при 
получим
. (4)
Если существует каждый из пределов, стоящих а правой части то, существует и предел, стоящий в правой части этого равенства, т.е. производная 
. Но 
и 
существуют по предположению.
Найдем 
, так как 
, а 
.
Учитывая это, формулу ( 4 ) можно записать в следующем виде
. (5)
Пример.Найти производную , если 
.
, 
, 
, 
.
