Рассмотрим функцию двух переменных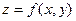 
.Зафиксируем один из аргументов, например, 
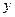, положив = 
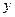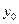.Тогда функция 
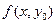будет функцией одной переменной 
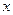.Пусть она имеет производную в точке 
:
.
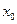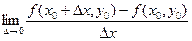Эта производная называется частной производной первого порядка функции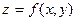 
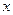по в точке Р 
. 
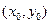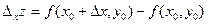- называется частным приращением по 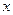функции 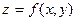в точке Р( 
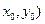.Тогда можно записать 
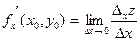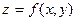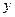, если этот предел существует. Аналогично определяются и обозначаются частное приращение функции по в точке Р( .
.
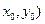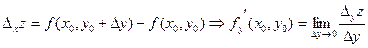Частные производные, рассматриваемые как функции двух переменных, обозначаются следующим образом:
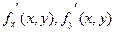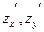или 
или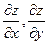 
.
Примеры.
Найти частные производные функций:
1. 
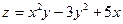
Частную производную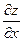 
находим как производную функции по аргументу 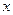в предположении, что 
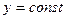. Поэтому 
.
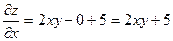Аналогично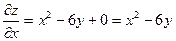 
.
2. 
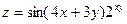
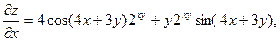
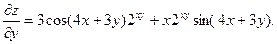
3. 
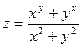
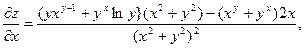
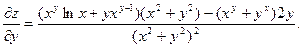
4. 
, 
, 
.
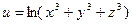
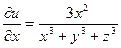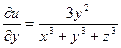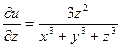