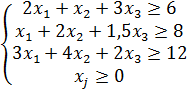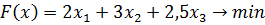Пусть для некоторых нужд, например кормления, требуется составить 2 вида корма, стоимость единицы каждого из которых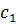 
и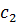 
. В каждом виде корма должны присутствовать питательные вещества 
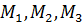, для которых известно, что в норме их должно быть не менее 
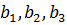единиц соответственно. Кроме того, известны технологические коэффициенты 
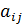- количество i-го питательного вещества в j-м виде корма. Требуется составить такой рацион питания, при котором стоимость корма была наименьшей, а количество питательных веществ не было бы меньше нормы.
Пусть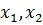 
- количество единиц корма каждого вида.
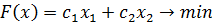
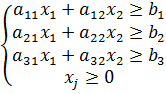
Пример. На свиноферме производится откорм свиней. Известно, что каждая должна получать не менее 6 единиц вещества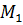 
, не менее 8 - 
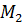, не менее 12 - 
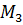. Существуют 3 вида кормов.
Информация по стоимости этих кормов и содержанию единиц каждого вещества в единице корма находится в таблице:
| Вид корма
| Вещества
| Стоимость
вида корма
|
|
|
|
|
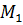
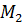
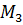
| 2
| 1
|
|
|
|
|
| 2
|
|
|
|
|
| 1,5
|
| 2,5
|
Требуется обеспечить наиболее дешевый рацион питания животных в виде комбикорма.
Решение. Пусть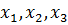 
- количество единиц корма каждого вида. Тогда математическая модель задачи имеет вид:
