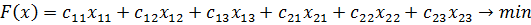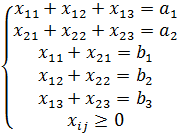В таких задачах, как правило, рассматриваются проблемы экономичной перевозки грузов или рационального распределения трудовых ресурсов по рабочим местам.
Пусть два поставщика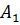 
и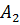 
, имеющих запасы груза в объеме 
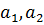должны переправить его потребителям 
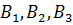. которым требуются объемы 
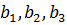. Известны стоимости перевозок от каждого поставщика к каждому потребителю (см. таблицу). Требуется составить такой план перевозок, при котором все грузы были бы вывезены, все потребители - удовлетворены, а стоимость перевозок была бы минимальной.
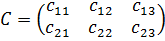- матрица стоимостей перевозок.
Не вдаваясь пока в специфику транспортных задач, предположим, что количество имеющихся и количество требуемых грузов совпадает.
Пусть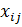 
- количество единиц груза, перевозимое от i-го поставщика j-му потребителю. Стоимость перевозок должна быть минимальной. Учитывая запасы поставщиков и нужды потребителей, составляем систему ограничений. Тогда математическая модель задачи имеет вид
