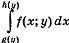Теорема о среднем, значении
Если функция f(x; у) непрерывна на области Р, то существует такая точка (а; b) 
Р , что
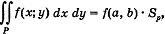
где Sp - площадь области Р.
Сведение двойных интегралов к повторным
Теорема 1. Пусть Р - плоская область, ограниченная графиками непрерывных функций g(x) и h(x), таких что g(x) 
h(x), х [а; b], и, быть может, отрезками прямых х = а и x = b. Если функция f(x; у) непрерывна в области Р, то
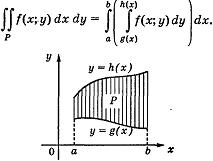
Интеграл, стоящий в правой части формулы, называется повторным интегралом и записывается в виде
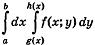
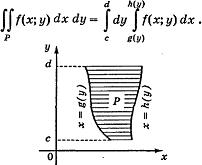
Отметим, что если плоская область Р ограничена графиками непрерывных функций g(y) и h(y), таких что g(y) h(y), у [с; d], и, быть может, отрезками прямых у = с и у = d, то порядок интегрирования может быть иным
Замечание. Расчет двойных интегралов приводит к необходимости вычисления выражений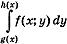 
, в которых интегрирование ведется по переменной у, а переменная х при этом играет роль константы (как, впрочем, и любое выражение р(х), зависящее только от х).
Пусть
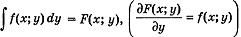
тогда
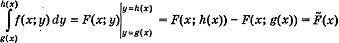
Аналогичным образом осуществляется интегрировала ние выражений вида
