Двойной интеграл обладает следующими свойствами:
1. 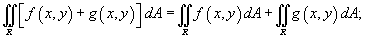
2. 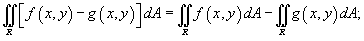
3.  , где k - константа;
, где k - константа;
4. Если  в области R, то
в области R, то  ;
;
5. Если  в области R и
в области R и  (рисунок 4), то
(рисунок 4), то  ;
;
6. Если  на R и области R и S являются непересекающимися (рисунок 5), то
на R и области R и S являются непересекающимися (рисунок 5), то  .
.
Здесь 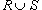 означает объединение этих двух областей.
означает объединение этих двух областей.
| Пример
|
| |
Пусть R и S являются непересекающимися областями (рисунок 5). Известны значения двойных интегралов:
 Оценить интеграл
Оценить интеграл  .
Решение.
Используя свойства двойных интегралов, получаем: .
Решение.
Используя свойства двойных интегралов, получаем:

|