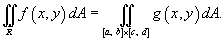Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как
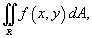
где R - область интегрирования в плоскости Oxy. Если определенный интеграл 
от функции одной переменной 
выражает площадь под кривой f (x) в интервале от x = a до x = b, то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости Oxy в области интегрирования R
Формально двойной интеграл можно ввести как предел суммы Римана. Пусть, для простоты, область интегрирования R представляет собой прямоугольник 
(рисунок 2). Используя ряд чисел{ x0, x1, ..., xm }, разобьем отрезок [a, b] на малые интервалы таким образом, чтобы выполнялось соотношение
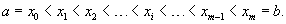
Аналогично, пусть множество чисел 
является разбиением отрезка [c, d] вдоль оси Oy, при котором справедливы неравенства
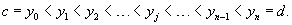
Суммой Римана функции f (x,y) над разбиением называется выражение
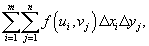
где 
- некоторая точка в прямоугольнике 
и 
.
Двойной интеграл от функции f (x,y) в прямоугольной области определяется как предел суммы Римана, при котором максимальные значения Δxi и Δyj стремятся к нулю:
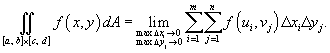
Чтобы определить двойной интеграл в произвольной области R, отличной от прямоугольной, выберем прямоугольник , покрывающий область R (рисунок 3), и введем функцию g (x,y), такую, что
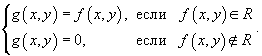
Тогда двойной интеграл от функции f (x,y) в произвольной области R определяется как
