Условный экстремум. Метод множителей Лагранжа.

Определение 3. Пусть Е - множество точек X n-мерного евклидова пространства Eⁿ, для которых выполняются условия

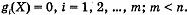
Точка Х₀ Еⁿ называется точкой условного экстремума функции у = f(X) относительно соотношений g_i(X) = 0, если она является точкой обычного экстремума этой функции, рассматриваемой только на множестве Е.
Если система уравнений g_i(x₁, х₂;...; x_n) = 0,i = l,2,..., m; m n-m+1;...; х_n:

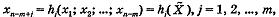
то вопрос об условном экстремуме функции у = f(x₁, х₂;...; x_n) равносилен вопросу об обычном экстремуме функции

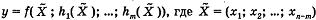
На практике, однако, или принципиально невозможно выразить из уравнений g_i(X) = 0 группу переменных, или это может оказаться слишком громоздкой операцией. В этом случае можно эффективно использовать метод множителей Лагранжа.

Определение 4. Функция , где - постоянные множители, называется функцией Лагранжа.

Теорема 6. Если в точке Х₀ выполняются условия: , точка Х₀ является стационарной точкой для функции Лагранжа, и если второй дифференциал функции Лагранжа в этой точке является положительно (отрицательно) определенной квадратичной формой переменных dx₁, dx₂,..., dx_nпри условии, что они удовлетворяют соотношениям

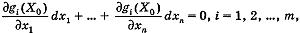
то точка Х₀ является точкой условного строгого минимума (максимума) для функции у = f(X) относительно условий g_i(X) = 0.

Геометрические приложения (Касательная прямая и нормальная плоскость к пространственной кривой, к поверхности заданной явно, к поверхности заданной неявно).