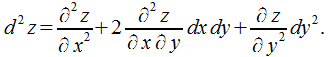В общем случае частные производные 
функции 
- это функции от 
и 
. В случае, если они дифференцируемы, то существуют четыре частные производные, которые имеют название частных производных второго порядка:
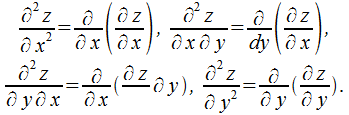
Подобным образом используются частные производные тертьего, …, n-го порядка.
О: в качестве частной производной n-го порядка представляется производная первого порядка от частной производной 
- го порядка.
Пример 1:
◀ 
▶
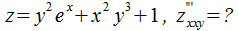
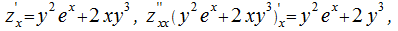
Пример 2:
◀ 
▶
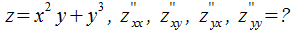
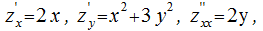
Заметим, что смешанные производные 
и 
, разница между которыми заключается в порядке дифференцирования, являются эквивалентными. В данном случае уместно записать теорему.
Т: Частные производные с разным порядком дифференцирования можно назвать равными в т. 
, если они в этой точке являются непрерывными.
Допустим,
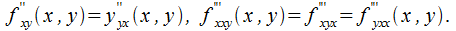
О: Под дифференциалом второго порядка понимают дифференциал от ее дифференциала первого порядка, который рассматривается в качестве функции переменных и при определенных значениях 
и 
.
Подобным образом находятся дифференциалы третьего, …, n-го порядка:
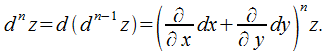
Выражение, заключенное в скобки, формально раскрывается в соответствии с биномиальным законом. Допустим,
