Одним из эффективных методов преобразования дифференциальных выражений является переход к новым переменным. Рассмотрим наиболее важные в практическом отношении случаи.
1. Преобразуемое выражение содержит обыкновенные производные:
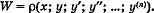
Если необходимо перейти к новому аргументу t и новой функции и, которые связаны с х и у соотношениями:
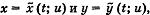
то надо подставить эти выражения в W вместе с производными
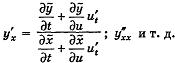
2. Преобразуемое выражение содержит частные производные:
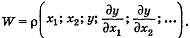
При переходе к новым аргументам t1 и t2, которые связаны со старыми х1 и х2 соотношениями:
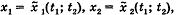
необходимо подставить эти выражения в W вместе с частными производными, которые определяются из следующих уравнений
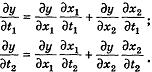
Частные производные высших порядков вычисляются аналогично.
Одним из эффективных методов преобразования дифференциальных выражений является переход к новым переменным. Рассмотрим наиболее важные в практическом отношении случаи.