Т е о р е м а 1. Если функция 
имеет производную в точке 
, а функция 
имеет производную в точке 
, то сложная функция 
(1)
имеет производную (по ) в точке и справедливо равенство
(2)
или
. (3)
Д о к а з а т е л ь с т в о. Зададим , ему соответствует значение 
. Придадим приращение 
, это вызовет приращение 
. Так как функция имеет производную в точке , то на основании равенства (2) § 4.1, имеем
, (4)
где 
при 
.
Будем считать, что 
. Равенство (4) при этом соглашении выполняется, т. к. если подставить в него 
, то получится 
.
Разделим теперь равенство (4) на :
. (5)
Пусть 
стремится к нулю. Тогда , потому что функция 
имеет производную в точке и, следовательно, непрерывна.
Переходим в равенство (5) к пределу при 
. Тогда и , поэтому получим
.
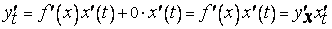Теорема доказана.
Формула (1) может быть усложнена. Например, если 
, 
, 
и все три функции имеют производные в соответствующих точках, то 
.
П р и м е р 1. 
.
Полагаем 
, 
, 
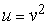. Тогда
.
П р и м е р 2.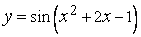 
.
Полагаем 
. Тогда
.
Обычно при вычислениях вспомогательные переменные 
не вводят, а только подразумевают их.
В случае примера 1 вычисления выглядят так:
.
Или еще короче
.
