N-мерное евклидово пространство.

Определение 1. Упорядоченная последовательность n действительных чисел {х₁, х₂;...; х_n} называется точкой п- мерного пространства, при этом числа x_i, i = 1,..., n называются координатами точки.
Обозначение: X = (х₁, х₂;...; х_n).

Определение 2. Если для любых двух точек X = (х₁, х₂;...; х_n) и У = (y₁, y₂;...; y_n) n-мерного пространства определено расстояние между ними по формуле

,

то такое пространство называется n-мерным евклидовым.
Обозначение: Еⁿ.

Определение 3. Пусть X - фиксированная точка пространства Еⁿ; > 0 - произвольное положительное число. Множество точек Y пространства Еⁿ таких, что

р(Х; Y) ,

называется n-мерным шаром с центром в точке X и радиусом или просто -окрестностъю точки X в пространстве Еⁿ.

Определение 4. Если существует отображение множества натуральных чисел в множество точек пространства Еⁿ

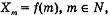
то множество точек Х₁; Х₂; ... называется последовательностью точек этого пространства.
Обозначение: {Х_m}.

Определение 5. Точка X Еⁿ называется пределом последовательности {Х_m}, если

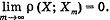
Определение 6. Пусть Е Еⁿ - некоторое подмножество n-мерного евклидова пространства. Отображение точек множества Е в множество действительных чисел R называется функцией п переменных.
Обозначение: у = f(х₁, х₂;...; х_n); у = f(Х).
Множество Е называется областью определения функции n переменных.