Формула интегрирования по частям для определённого интеграла.
Пример Вычислим интеграл
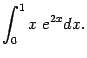
Выгодно взять 
и 
, так что получаем:
При этом возникший по дороге внеинтегральный член 
мы вычислили так:
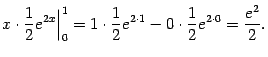
Особенно ясно проявляется указанное в замечании преимущество в том случае, если формулу интегрирования по частям приходится применять несколько раз подряд. Равномерное приближение непрерывной функции тригонометрическими и алгебраическими многочленами. 2-ая теорема Вейерштрасса. Интеграл Фурье и его свойства.
Преобразование Фурье, понятие об обратном преобразовании Фурье. Аналог признака Дини (без доказательства). Синус и косинус- преобразования Фурье.
