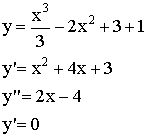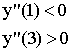Функция называется возрастающей если большему значению аргумента соответствует большее значение функции, а меньшему соответствует меньше.
Функция называется убывающей если большему значению аргумента соответствует меньшее значение функции, а меньшему соответствует большее.
Теорема. У возрастающей функции производная больше 0 ( 
).
Доказательство:
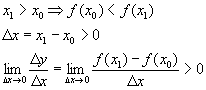
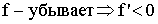
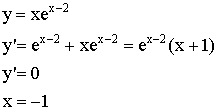
Экстремумы функции.
Точка 
-называется точкой max, если существует некоторая окрестность точки, что для любой точки x из этой окрестности 
.
Точка -называется точкой min, если существует некоторая окрестность точки, что для любой точки x из этой окрестности 
.
Необходимый признак экстремума, если -точка экстремума.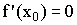 
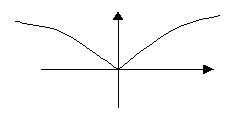
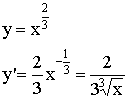
Если 
и 
, то это точка экстремума.
Если - точка экстремума и существует , то производная =0. Точка, в которой производная, равна нулю, называется критической точкой.
, теорема Логранжа.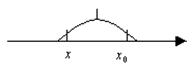 
Первый достаточный признак экстремума.
Если при переходе через критическую точку производная меняет знак с ”+” на “-“,то в этой точке максимум.
Если при переходе через критическую точку производная меняет знак с ”-” на “+“,то в этой точке минимум.
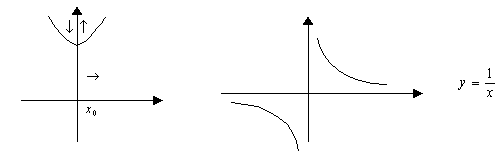
Второй достаточный признак экстремума.
Если в критической точке 2-ая производная больше нуля, то это точка минимума, а если в критической точке 2-ая производная меньше нуля, то это точка максимума.
Пример:
