Задача.

В таблице представлены данные по некоторой бригаде, где признак Х − трудовой стаж и Y − разряд.

1. Для признака Х построим вариационный ряд. Для этого расположим данные в порядке возрастания: 5, 5, 5, 5, 6, 7, 7, 8, 9, 9.

2. Полигоном называется ломанная линия, соединяющая точки (x₁, n₁), (x₂, n₂),.., (x_r, n_r), гдеn_i − частота значения х_i.

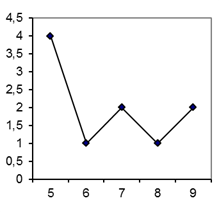
Рис.1 Полигон распределения

3.1 Мода распределения – это наиболее часто встречающееся значение ряда.

3.2 Выборочное среднее находится по формуле

= (х₁+х₂+х₃+.. +х_n)/n.

Средний стаж равен (8+9+5+7+5+7+9+5+6+5)/10=6,6.

4.1 Выборочная дисперсия распределения находится по формуле:

.

В нашем примере .

4.2 Оценка стандартного отклонения определяется как корень квадратный из выборочной дисперсии: .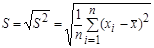

4.3 Формула коэффициента вариации: .

Если С_v≤ 10%, то варьирование считается слабым,

при 11% ≤ С_v≤ 25% - средним, и значительным при С_v> 25%.

5. Доверительный интервал для оценки среднего значения нормального распределения при неизвестной дисперсии:

,

где - выборочная дисперсия, а значение находят по таблице “Квантили распределения Стьюдента”.