В таблице представлены данные о работниках бригады: разряд (Х) и стаж работы (Y, лет).
Чаще всего, чем больше стаж работы, тем выше квалификация рабочего и, следовательно, выше его разряд. Поэтому в нашем примере стаж работы (Х) – независимая переменная, а разряд (Y) – зависимая от Х переменная.
Для построения корреляционного поля (диаграммы рассеивания) на координатную плоскость нанесем точки с координатами (1; 1), (1; 2), (2; 3), (3; 4), (6; 5) (рис.2). По конфигурации скопления точек мы можем предположить, что связь между стажем и разрядом есть, причем скорее всего эта связь линейная и положительная.
Найдем коэффициент линейной корреляции. Для удобства представим наши вычисления в виде следующей таблицы:
| хi
| yi
| 
| 
| xiyi
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ∑ = 13
|
|
|
|
|
n = 5.
Выборочный коэффициент корреляции мы будем находить по следующей формуле:
 .
.
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Полученное значение коэффициента r = 0,92 очень близко к 1, что указывает на сильную зависимость между стажем и разрядом рабочего.
Построим линию регрессии Y на Х.
 ,
,
 ,
,
y =0,7х + 1,17.
Получаем следующий график.
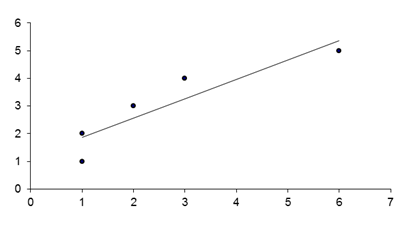
Рис.2