Пусть один и тот же опыт повторяется 
раз, испытания независимы, в результате каждого испытания может наступить или нет событие 
. Пусть 
- вероятность наступления , тогда 
. Такая схема испытаний называется схемой Бернулли. Найдём вероятность 
того, что событие произойдёт при испытаниях 
раз.
Пространство элементарных событий состоит из произведений событий или 
: 
, 
, 
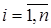. Событие 
, состоящее в том, что событие произойдёт при испытаниях раз включает те 
, в которых содержится раз, их 
. По формуле (13.7): 
, поэтому по (12.3) 
. Формула
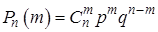(13.10)
называется формулой Бернулли.
Пример. Найти вероятность того, что четырехзначный номер первого встречного автомобиля содержит две цифры 5.
Решение. Так как 
, (число цифр в номере), 
, событие - данная цифра номера 5, - не 5, 
, 
, то 
.
При больших значениях , подсчёт проводят по приближённой формуле(локальная теорема Лапласа)
, 
, 
.
Если велико, а 
, 
, то применяют приближённую формулу Пуассона:
, 
. (13.11)
Последнюю формулу называют законом редких событий.
