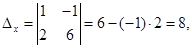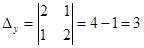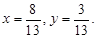Системой 
линейных алгебраических уравнений с 
неизвестными является система:
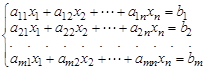
Пример.
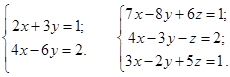
Основной матрицей системы называется матрица из коэффициентов:
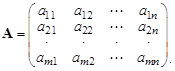
Введём также матрицы столбцы неизвестных и свободных членов
, 
.
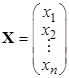Тогда систему можно записать в матричной форме: 
.
О: Решением системы называется любой набор чисел 
, который при подстановке в уравнения системы вместо соответствующих неизвестных обращает их в тождества. Система называется совместной, если она имеет решение, несовместной, если решения нет. Совместная система называется определённой, если решение единственно и неопределённой, если решений бесконечно много.
Решить систему - это значит найти все значения неизвестных, которые при подстановке в уравнения системы превращают их в правильные равенства (тождества). Система линейных уравнений может иметь одно решение, бесконечное множество решений или вообще не иметь решений.
При решении систем линейных уравнений можно использовать методы Гаусса, Крамера или метод обратной матрицы.
Метод Крамера.
Разберем этот метод решения на примере системы
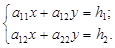
Вычислим основной определитель системы
и определители 
и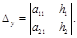 
Тогда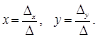 
Метод применим если основной определитель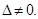 
При 
система имеет бесконечно много решений, если
,
и не имеет решения, если хотя бы один определитель 
.
Пример. Решить систему
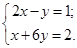
Решение.
