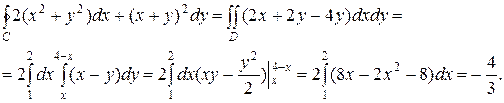Зв'язок між подвійним інтегралом за областю D і криволінійним інтегралом по границі С цієї області встановлює формула Остроградського-Гріна.
Означення. Область називається однозв'язною, якщо будь-який замкнений контур, що втримується в цій області можна стягти в точку не виходячи за межі області.
ТЕОРЕМА. Якщо функції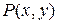 
й 
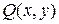та їхні частинні похідні 
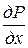та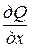 
неперервні в деякій однозв'язній області D, обмеженій простим замкнутим контуром С, то має місце формула:
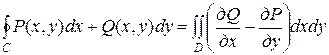. (5.6)
Нехай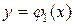 
– рівняння дуги АnВ, а 
– рівняння дуги АmВ (Рис. 26).
Знайдемо спочатку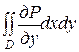 
. За правилом обчислення подвійного інтеграла маємо:
.
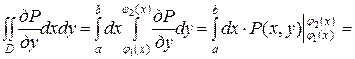
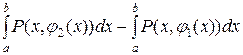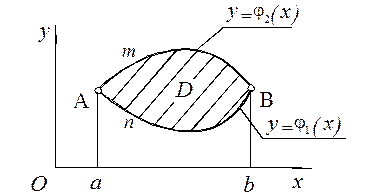
Рис. 26
Якщо звести до інтеграла за замкнутим контуром, то отримаємо:
= 
.
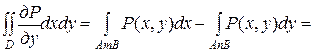
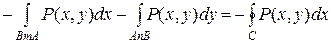Аналогічно доводиться, що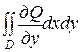 
= 
.
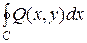Зауваження 1. Формула Гріна справедлива і для довільної замкненої області, яку можна розбити на скінченне число правильних замкнених областей.
Зауваження 2. Формула Гріна справедлива для довільної області обмеженої одним або кількома кусково-гладкими контурами.
Приклад. Застосовуючи формулу Остроградського-Гріна, обчислити інтеграл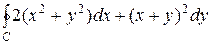 
, де С – контур трикутника з вершинами L (1, 1), M (2, 2), N (1, 3) (Рис. 27).
Розв’язання. Знайдемо частинні похідні:
,
.
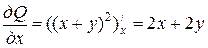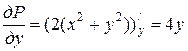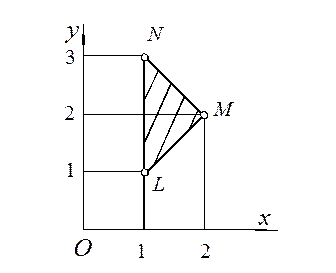
Рис. 27
Складемо рівняння прямих, що належать області D:
LM: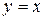 
, MN: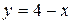 
.
