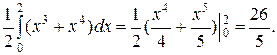Крива задана у параметричному вигляді.

Якщо крива АВ задана параметричними рівняннями 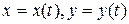, де функції 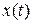й 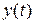неперервні разом зі своїми похідним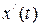и й 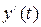на відрізку[t₁, t₂], причому початковій точці А кривій відповідає значення параметра t₁, а кінцевій точці В – значення t₂ , тоді:

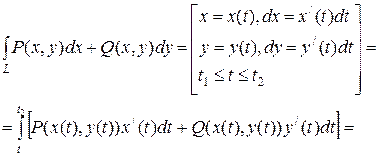
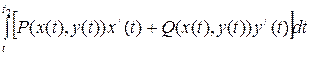= . (5.4)

Якщо АВ – гладка просторова крива, що описується неперервними функціями 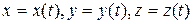на деякому відрізку [t₁, t₂], то криволінійний інтеграл обчислюється за формулою:

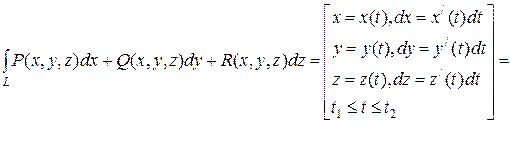
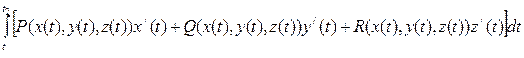= . (5.5)

Приклад. Обчислити інтеграл 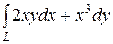, від точки О (0, 0) до точки А (2, 1).де крива L задана рівнянням .

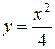Розв’язання.

= =

=
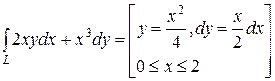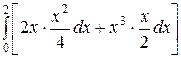