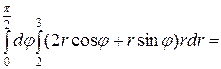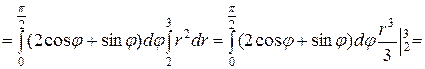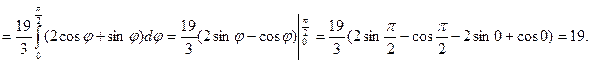|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Подвійний інтеграл у полярних координатахДата добавления: 2015-08-31; просмотров: 6196; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

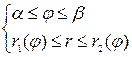 . Область D називається правильною областю в полярній системі координат, якщо кожний промінь, який виходить з полюса, перетинає границю області не більш ніж у двох точках. Сумістимо полярну систему координат з декартовою так, щоб полюс полярної системи збігався з початком координат, а полярною віссю служитиме вісь ОХ (Рис.12, а). За означенням подвійного інтеграла маємо:
. Область D називається правильною областю в полярній системі координат, якщо кожний промінь, який виходить з полюса, перетинає границю області не більш ніж у двох точках. Сумістимо полярну систему координат з декартовою так, щоб полюс полярної системи збігався з початком координат, а полярною віссю служитиме вісь ОХ (Рис.12, а). За означенням подвійного інтеграла маємо: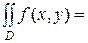
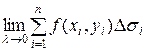 .
.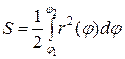 ):
):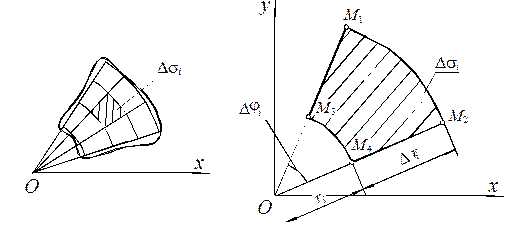
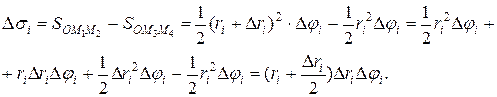
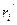 середній радіус між ri і r i + Dr і, тобто
середній радіус між ri і r i + Dr і, тобто 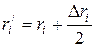 . Тоді:
. Тоді: 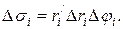
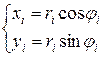 , отримаємо:
, отримаємо: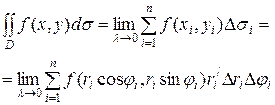 .
.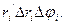 Але можна довести, що помилка від такої заміни в межах зведеться до нуля.
Але можна довести, що помилка від такої заміни в межах зведеться до нуля.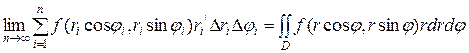 .
.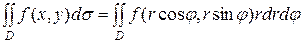 . (2.9)
. (2.9)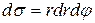 називається елементом площі в полярних координатах. З точністю до нескінченно малих більш високого порядку малості ніж
називається елементом площі в полярних координатах. З точністю до нескінченно малих більш високого порядку малості ніж 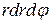 , він дає площу
, він дає площу 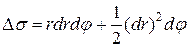 криволінійного чотирикутника, зображеного на Рис. 12, б так як
криволінійного чотирикутника, зображеного на Рис. 12, б так як 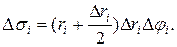
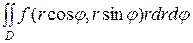 застосовують також правило зведення його до повторного інтегралу, але тільки тут роль змінних грають r і φ.
застосовують також правило зведення його до повторного інтегралу, але тільки тут роль змінних грають r і φ.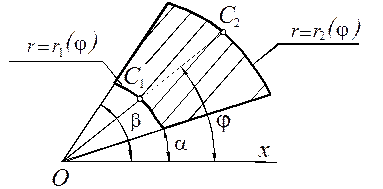
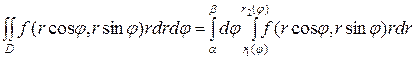 . (2.10)
. (2.10)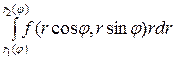 обчислюється при постійному j. Результатом цього інтегрування буде деяка функція від змінної j, яку потім потрібно інтегрувати на границях від a до b. Межами зовнішнього інтегрування є значення a і b, між якими змінюється полярний кут, коли точка пробігає область D.
обчислюється при постійному j. Результатом цього інтегрування буде деяка функція від змінної j, яку потім потрібно інтегрувати на границях від a до b. Межами зовнішнього інтегрування є значення a і b, між якими змінюється полярний кут, коли точка пробігає область D.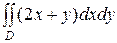 , якщо область визначення обмежена лініями:
, якщо область визначення обмежена лініями: 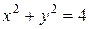 ,
, 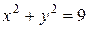 , х ³ 0, у ³ 0.
, х ³ 0, у ³ 0.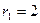 та
та 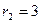 , а умова х ³ 0, у ³ 0 показує, що область лежить у першій чверті координатної площини, тобто кут j змінюється від 0 до
, а умова х ³ 0, у ³ 0 показує, що область лежить у першій чверті координатної площини, тобто кут j змінюється від 0 до 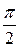 .
.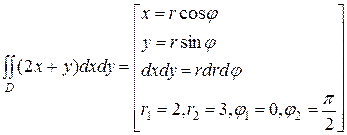 =
=