Розглянемо двократний інтеграл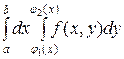 
. Якщо область інтегрування D задана нерівностями 
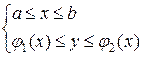(Рис. 10, а) і є також правильною відносно осі ОУ, тобто границя області D перетинається прямою у = с, де (с = const) не більш як у двох точках, то область D можна задати іншими нерівностями: 
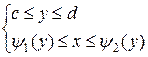. Тут c і d – відповідно найбільше та найменше значення у в області D, х = y1(у) – ліва частина границі, х = y2(у) – права частина границі області D (Рис. 10, б). Тоді в двократному інтегралі можна змінити порядок інтегрування: 
.
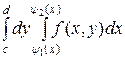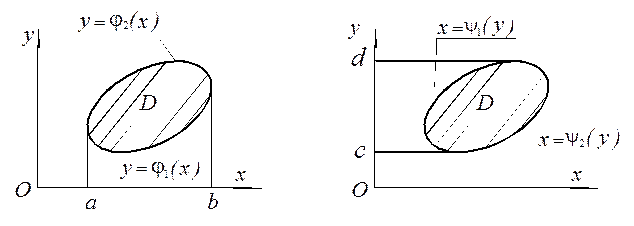
а б
Рис. 10
Приклад. Змінити порядок інтегрування у двократному інтегралі:
.
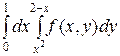Розв’язання. Визначимо границі області D: а = 0, b = 1, y1 = x2, y2 = 2 – x,(Рис. 11, а).
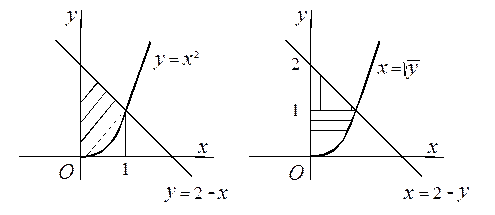
а б
Рис. 11
Область D є простою в напрямку осі ОУ, так як довільна пряма, паралельна осі ОУ, перетинає границю області не більш як у двох точках. При зміні порядка інтегрування лінія входу має рівняння х = 0, а лінія виходу розбивається на дві частини, одна з яких має рівняння х =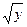 
, а друга – рівняння х = 2 – у. За властивістю адитивності подвійного інтеграла він розбивається на два (Рис. 11, б):
В кожному з інтегралів в яких зроблена заміна на повторний інтеграл з внутрішнім інтегруванням за змінною х, а зовнішнім інтегруванням за змінною у:
.
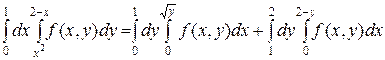