Розглянемо інтеграл за фігурою залежно від заданої фігури по який обчислюється інтеграл.
1. Якщо фігура Ф є відрізком прямої [a, b] на осі ОХ (f(P) = f(х), dm = dх), то інтеграл за фігурою перетворюється у звичайний визначений інтеграл на проміжку [a, b]:  .
.
2. Якщо фігура Ф є лінією L (f(P) = f(х, y), dm = dL), то інтеграл за фігурою перетворюється в криволінійний інтеграл за довжиною дуги:
 .
.
3. Якщо фігура Ф є плоскою областю D (f(P) = f(х, y,), dm = ds), то інтеграл за фігурою перетворюється в подвійний інтеграл:
 .
.
4. Якщо фігура Ф є областю поверхні Q (f(P) = f(х, y, z(х, у)), dm = dq), то інтеграл за фігурою перетворюється в поверхневий інтеграл:
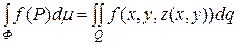 .
.
5. Якщо фігура Ф є об'ємним тілом R у просторі (f(P) = f(х, y, z), dm = dv), то інтеграл за фігурою перетворюється в потрійний інтеграл:
 .
.