Властивості інтеграла за фігурою

1. Властивість лінійності.

Інтеграл від алгебраїчної суми скінченої кількості інтегрованих в області функцій дорівнює алгебраїчній сумі інтегралів від цих функцій, тобто

.

2. Постійний множник можна виносити за знак інтеграла, тобто

.

3. Властивість адитивності за областю інтегрування.

Якщо фігуру Ф розбити на кілька частин (Ф = Ф₁ + Ф₂), то інтеграл за цілою фігурою дорівнює сумі інтегралів цих частин, тобто

.

4. Властивість монотонності функції (інтегрування нерівності).

Якщо в кожній точці фігури 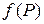≤ , то .

5. Середнє значення функції.

Якщо , то .

6. Властивість міри.

Якщо функція f(P) тотожньо дорівнює одиниці в кожній точці фігури:

(f(P) 1), то інтеграл від неї за фігурою дає міру самої фігури, тобто

.