Формула Тейлора имеет много приложений и является основой приближенных вычислений. Поскольку наиболее простыми функциями являются многочлены, то возникает вопрос о возможности замены функции 
в окрестности точки х0 многочленом некоторой степени.
Пусть функция определена в некоторой окрестности точки х0 и имеет в этой точке n производных 
, 
, …, 
.
Требуется найти многочлен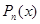 
степени не выше n, такой, что
(1),
где 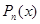удовлетворяет условиям: 
, 
, …, 
.
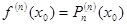Таким многочленом является
– многочлен Тейлора функции .
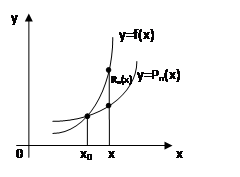
Многочлен 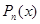удовлетворяет условию (1), то есть 
. Обозначим 
– погрешность при замене многочленом .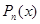
Теорема. Если функция 
определена и n раз дифференцируема в окрестности точки х0, то при 
имеет место формула
– формула Тейлора с остаточным членом 
в форме Пеано.
Замечание. 
где 
– формула Тейлора с остаточным членом в форме Лагранжа.
Пусть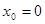 
, тогда формула Тейлора примет вид
– формула Маклорена (формула Тейлора-Маклорена) где 
задается в форме Пеано ( 
) или в форме Лагранжа (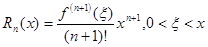 
).
