I. Параметрическое задание функций.
Пусть 
, 
– две функции одной независимой переменной 
. Если – монотонна на Т, то существует обратная к ней 
. Тогда получим 
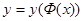– сложную функцию y от x. В этом случае говорят, что функция y от x задана параметрически и пишут 
, 
, t – параметр.
Параметрическое задание часто применяют при описании траектории движения точки на плоскости, где координаты х и у – функции времени t. Иногда от параметрического задания функции можно перейти к явному, исключив параметр t. Всегда функцию, заданную явно 
можно задать параметрически:
, .
II. Параметрическое задание некоторых линий на плоскости.
, . Каждому значению соответствует определенное значение х и определенное значение у 
соответствует точка М(х,у). Когда t пробегает все значения из Т, точка М(х,у) описывает некоторую линию на плоскости Оху.
Рассмотрим параметрическое задание некоторых линий
Прямая
, 
2) Окружность с центром О(0;0) и радиусом а.
, 
,
параметр t – угол между положительным направлением оси Ох и 
, М(х,у) принадлежит окружности.
Эллипс
,
