Рассмотрим новое правило раскрытия неопределенностей 
и 
.
Теорема 1. Пусть функции 
и 
дифференцируемы в окрестности точки х0, за исключением, быть может, самой точки х0, причем в этой окрестности 
. Пусть 
. Тогда, если существует 
, то существует и 
, причем 
(1).
Без доказательства.
Теорема 2. Пусть функции и дифференцируемы в окрестности точки х0, за исключением, быть может, самой точки х0, причем в этой окрестности . Пусть 
и 
. Тогда, если существует , то существует и , причем 
(2).
Без доказательства.
Смысл правила Лопиталя: вычисление предела отношения функций в случае неопределенностей или может быть сведено к вычислению предела отношений производных (который бывает проще).
Замечание1. Если 
(или ) и 
, 
удовлетворяют условиям теоремы 1 (или теоремы 2), то правило Лопиталя применяют еще раз
и т.д.
Замечание2. Теоремы 1 и 2 справедливы и при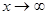 
.
Примеры:
1) 
, 
Другая форма записи (при условии существования ):
2) 
3) 
4) 
5) Формулы (1) и (2) справедливы, если 
! Может оказаться, что существует, а не существует.
Найти 
- не существует.
