Определение. Простейшими правильными дробями I, II и III типов называются следующие дроби:
I. 
;
II. 
; ( 
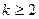- целое положительное число);
III. 
; (корни знаменателя комплексные, то есть: 
.
Рассмотрим интегралы от простейших дробей.
I. 
; (20)
II.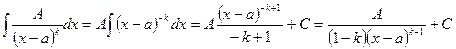 
; (21)
III.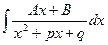 
;
Преобразуем числитель дроби таким образом, чтобы выделить в числителе слагаемое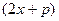 
, равное производной знаменателя.
= .
Рассмотрим первый из двух полученных интегралов и сделаем в нем замену:
.
Во втором интеграле дополним знаменатель до полного квадрата:
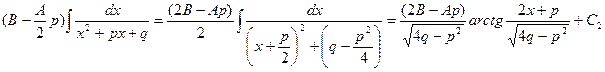
Окончательно, интеграл от дроби третьего типа равен:
= 
+ 
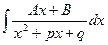. (22)
Таким образом, интеграл от простейших дробей I-го типа выражается через логарифмы, II –го типа – через рациональные функции, III-го типа – через логарифмы и арктангенсы.
