а) R(-sinx, cosx)=-R(sinx, cosx).
Если подынтегральная функция меняет знак при замене sinx на –sinx,то применяется подстановка cosx=t.
б) R(sinx, -cosx)=-R(sinx, cosx).
Если подынтегральная функция меняет знак при замене cosx на –cosx,то применяется подстановка sinx=t.
в) R(-sinx, -cosx)=R(sinx, cosx).
Если подынтегральная функция не меняется при изменении знаков у cosx и sinx,то применяется подстановка tgx=t (ctgx=t).
III.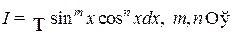 
1. Если n-нечётно, то применяется подстановка sinx=t.
Пусть n=2k+1, тогда
.
2. Если m=2k+1-нечётное, то применяется подстановка cosx=t.
Пример.
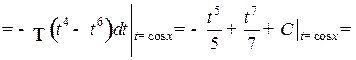
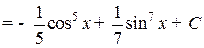
3. m+n=0
a) m>0
. Подстановка t=tgx.
б) n>0
. Подстановка t=ctgx.
4. m+n=-2k, k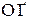 
a) m>0
.
Подстановка t=tgx.
б) n>0
.
Подстановка t=ctgx.
5. m, n-чётные неотрицательные числа. Применяются формулы понижения степени:
.
6. m, n-чётные, хотя бы одно из них неотрицательно. Применяется подстановка t=tgx или t=ctgx
IV. 
. Подстановка t=tgх.
. Подстановка t=ctgx.
V.a)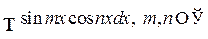 
б)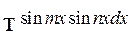 
в)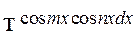 
Применим формулы: а) 
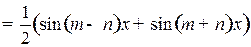
б) 
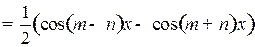
в) 
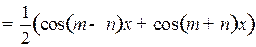
VI. 
. Подстановка t=ex. Отсюда x=lnt. Следовательно, 
. Тогда, 
-интеграл от рациональной функции от t.
II. Определенный интеграл
