Пусть даны точки A(4; 2; 5), B(0; 7; 2), C(0; 2; 7), D(1; 5; 0).
1. Треугольник ABC построен на векторах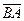 
и 
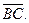Для вычисления площади основания ABC найдём векторное произведение этих векторов: 
. Площадь треугольника ABC равна 
модуля векторного произведения: 
2. Пирамида ABCD построена на векторах 
Объём пирамиды ABCD вычисляется как 
модуля смешанного произведения этих векторов: 
. Так как смешанное произведение векторов равно определителю, составленному из координат этих векторов, то 
. Тогда 
3. Длину высоты пирамиды DO, опущенную из вершины D на основание ABC, определим как расстояние от точки D до плоскости ABC. Для этого составим общее уравнение плоскости ABC. Будем использовать уравнение плоскости, проходящей через три точки A, B и C:
x+2y+2z-18=0.
Используя формулу нахождения расстояния от точки до прямой, получаем:
Итак, длина высоты DO равна 2.
