Теорема существования определенного интеграла (без доказательства).

Как видим, не всякая функция интегрируема на заданном отрезке. Однако имеет место следующая важная теорема: Если функция f(x) непрерывна на отрезке [a;b] то 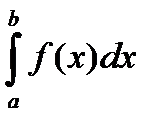существует, т.е. предел (1.2.2) существует и не зависит от способа разбиения отрезка [a;b] на частичные отрезки и от выбора точек 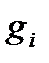на этих отрезках.

Большое практическое значение этой теоремы очевидно. Она, например, показывает, что всякая криволинейная трапеция, ограниченная сверху непрерывной кривой, обладает определенной площадью.