Определение. Гиперболой называется геометрическое место точек плоскости, для которых разность расстояний r1 и r2 до двух фиксированных точек F1 и F2, называемых фокусами, есть величина постоянная, равная 2а.
Введем декартову систему координат, как указано на рис. 1.
На основании определения гиперболы можно утверждать, что для всех точек М (х; у) гиперболы, и только для них, должно выполняться равенство
r1 – r2= ± 2а, (1)
которое в координатной форме принимает вид:
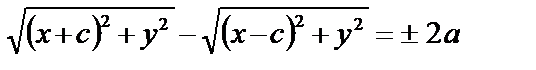 (2)
(2)
После упрощений, которые были сделаны при выводе канонического уравнения эллипса, вновь получим уравнение
(а2 – с2) х2 + а2у2 = а2(а2 – с2) (3)
в котором теперь разность а2 – с2 < 0 (разность двух сторон треугольника на рис. 1 меньше его третьей стороны, т. е. r1 – r2= 2а < 2c и а2 < c2. Поэтому положим
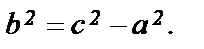 (4)
(4)
Тогда уравнение (3) после деления на а2b2приводится к виду
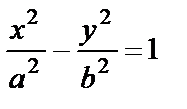 (5)
(5)
Уравнение (5) называется каноническим уравнением гиперболы.