1. Дифференциальное уравнение второго порядка, его общее решение и начальные условия.
Дифференциальное уравнение второго порядка,разрешенное относительно у", имеет вид:
 .
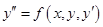| (6.41)
|
В общее решение уравнения второго порядка входят две произвольные постоянные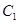 
и 
.
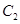Функция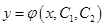 
, удовлетворяющая уравнению (6.41), называется его общим решением.
Рассмотрим два частных случая, когда уравнение второго порядка (6.41) сводится к дифференциальному уравнению первого порядка.
1) Пусть в правой части уравнения (6.41) отсутствует функция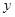 
и ее производная 
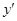, т.е. уравнение имеет вид
 .
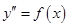| (6.42)
|
В результате двукратного последовательного интегрирования получаем общее решение этого уравнения:
 .
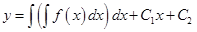| (6.43)
|
2) Пусть в правой части уравнения (6.41) отсутствует функция 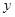, т.е. уравнение имеет вид
 .
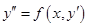| (6.44)
|
В этом случае обозначим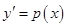 
, тогда 
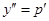. Подстановка этих выражений в уравнение (6.44) приводит его к уравнению первого порядка вида
 .
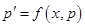| (6.45)
|
общим решением этого уравнения будет функция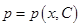 
. Отсюда получаем уравнение 
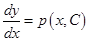или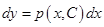 
.
Интегрируя последнее соотношение, получим общее решение уравнения (6.44):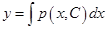 
.
6.7. Линейные однородные дифференциальные уравнения
