| №
| Задания
| Ответы
|
|
| 
|
|
|
| 
|
|
|
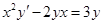
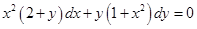
| 2. Найти решения задач Коши
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
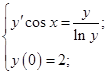
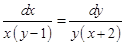
6.4. Однородные уравнения первого порядка
Уравнение вида (6.14) называется однородным уравнением первого порядка, если функция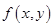 
представляется в виде функции, зависящей только от величины 
:
= 
.
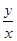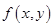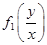Таким образом, однородное уравнение первого порядка имеет вид
 .
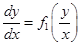| (6.27)
|
Для решения уравнения (6.26) используется подстановка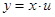 
, где 
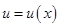- новая искомая функция. Производная 
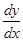находится по формуле нахождения производной произведения 
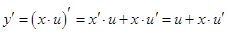, кроме этого 
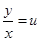. В результате подстановки последних выражений уравнение (6.27) преобразуется к виду
 .
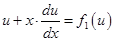| (6.28)
|
После переноса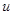 
в правую часть уравнение (9.28) превращается в уравнение с разделяющимися переменными
 .
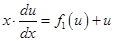| (6.29)
|
Разделение переменных приводит уравнение (6.29) к виду
 .
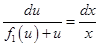| (6.30)
|
В результате интегрирования (6.30)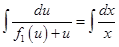 
получаем
 .
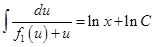| (9.31)
|
Здесь постоянная интегрирования представлена в виде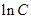 
для удобства записи окончательного ответа.
Дальнейший ход решения заключается в вычислении интеграла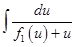 
при известной функции 
.
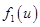Пример 6.7.
Найти общее решение уравнения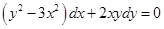 
.
Решение
,
, , 
,
, 
, 
,
, 
,
, 
, 
,
,
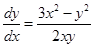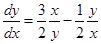
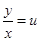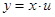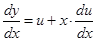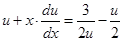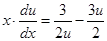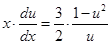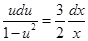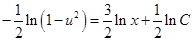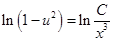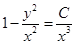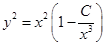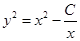Ответ:
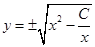, где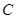 
– произвольная постоянная.
