Теория функциональных рядов общего вида является обобщением теории числовых рядов. Многие положения из числовых рядов с определенными оговорками переносятся на функциональные ряды.
Дан функциональный ряд 
. По аналогии с числовыми рядами введем понятие 
частичной суммы ряда
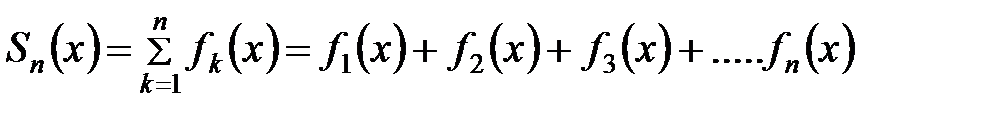
и его остатка 
.
Справедливой остается теорема, что из сходимости ряда следует сходимость его остатка и наоборот. Если ряд расходится, то расходится и его остаток, а из расходимости остатка следует расходимость ряда. Более того, если ряд сходится, то есть имеет конечную сумму 
, то 
. В самом деле, 
, но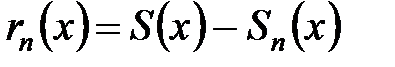 
, откуда следует
.
