Если числовые ряды в настоящее время используются, в основном для отработки методики исследования их сходимости, то функциональные ряды имеют широчайшее применение при решении различных уравнений, особенно в случаях, когда их точное решение построить не удается. Более того, решение уравнения в виде ряда считается точным, если сходимость ряда доказана. Не менее успешно используются функциональные ряды при вычислении приближенных значений некоторых функций. Точное значение даже такой простой функции, как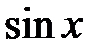 
, известно только для нескольких значений аргумента ( 
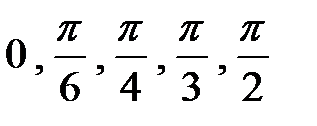и так далее). Чтобы подсчитать значение этой функции в промежуточных точках, используется представление 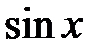в виде ряда. Кстати, при вычислении этой функции с помощью компьютера или микрокалькулятора фактически используется ее "разложение в ряд".
Широкую известность получили степенные ряды, ряд Фурье и различные его модификации.
